Plan de cours
consigne : à faire en classe
- Cours (lire et comprendre) : §1 p.304
- Activité 1 p.300 ou Exercice corrigé 8 p.307 et 9 p.307
- Exercices 1,13,16, p.306
Devoirs à la maison
- Visualiser les activités complémentaires PCCL, vidéo
- Applications vérification des connaissances
Exercices 1,13,16, p.306 et 22 p.311 - Cours et vocabulaire à apprendre (recopier ou résumer)
Cours et vocabulaire
Un objet abandonné sans vitesse initiale a un mouvement rectiligne vertical.
L’énergie qu’un système possède du fait de son mouvement s’appelle l’énergie cinétique. Elle est proportionnelle à la masse du système ainsi qu’au carré de sa vitesse.
Doubler la vitesse d’un système fait quadrupler son énergie cinétique.
L’énergie cinétique Ec (en Joules J) d’un système se déplaçant à la vitesse v (en m/s) et de masse m (en kg) est donnée par la relation ci-contre.
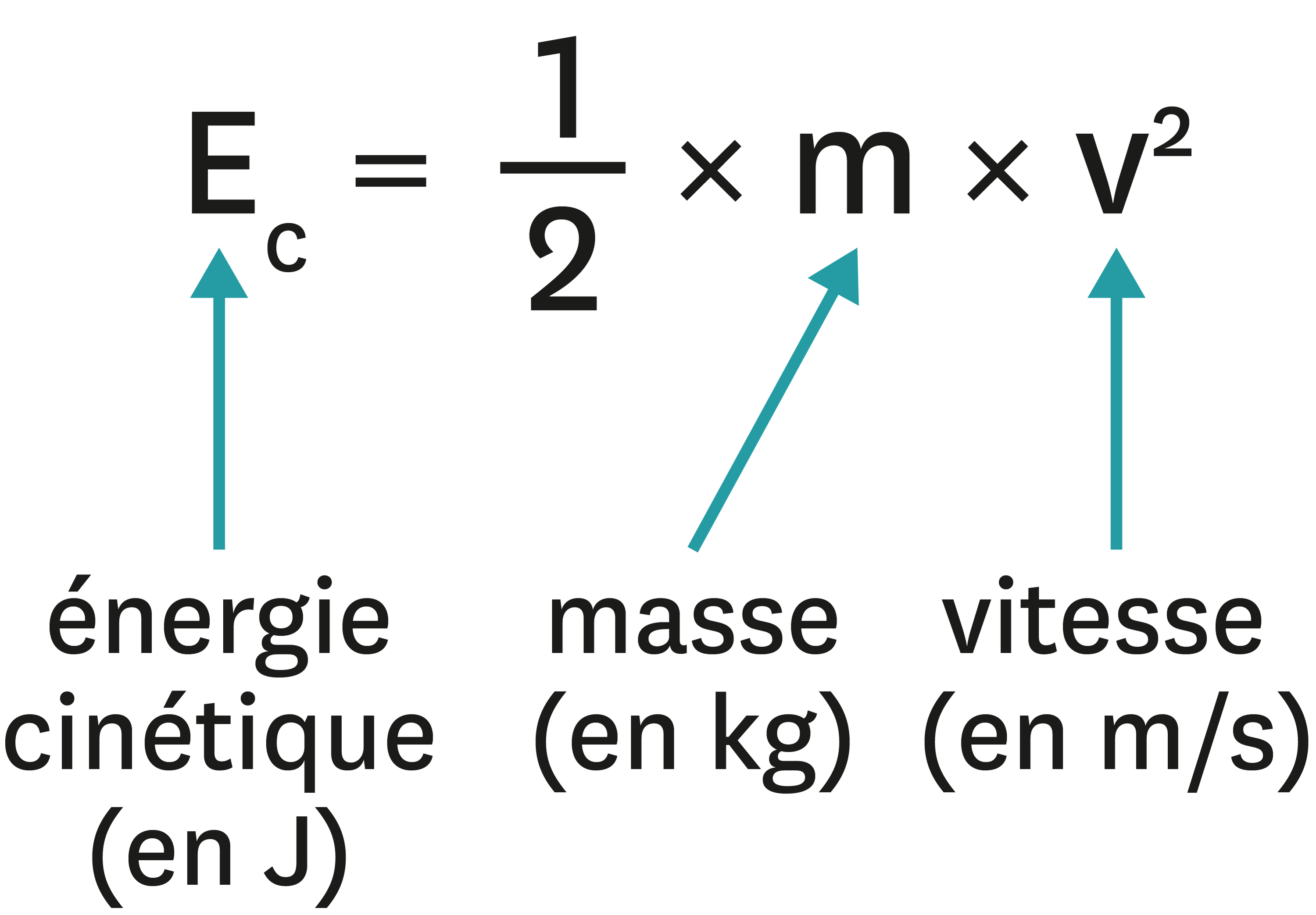
| Vocabulaire | Définition |
| cinétique | en mouvement (du grec : kinêtikos) |
Livre
Activités pour comprendre 1 p.300 – Comment augmente l’énergie cinétique (niveau 2GT – travail en autonomie)
Livre p.300

1 À ton avis, quel est le lien entre l’énergie cinétique et les grandeurs dont elle dépend ?
> une masse plus grande ou une vitesse plus élevée impliquent des impacts plus destructeurs
2 De quelles grandeurs physiques dépend l’énergie cinétique ?
> Le document 1 montre que l’énergie cinétique dépend de la masse du système qui est en mouvement et qui augmente avec elle. Le document 3 montre, quant à lui, que l’énergie cinétique d’un système en mouvement dépend de sa vitesse et augmente avec elle.
3 Trace la courbe représentant l’évolution de l’énergie cinétique en fonction de la masse du véhicule. Comment ces deux grandeurs sont-elles liées ?
> Le graphique tracé à partir des valeurs du tableau est le suivant :
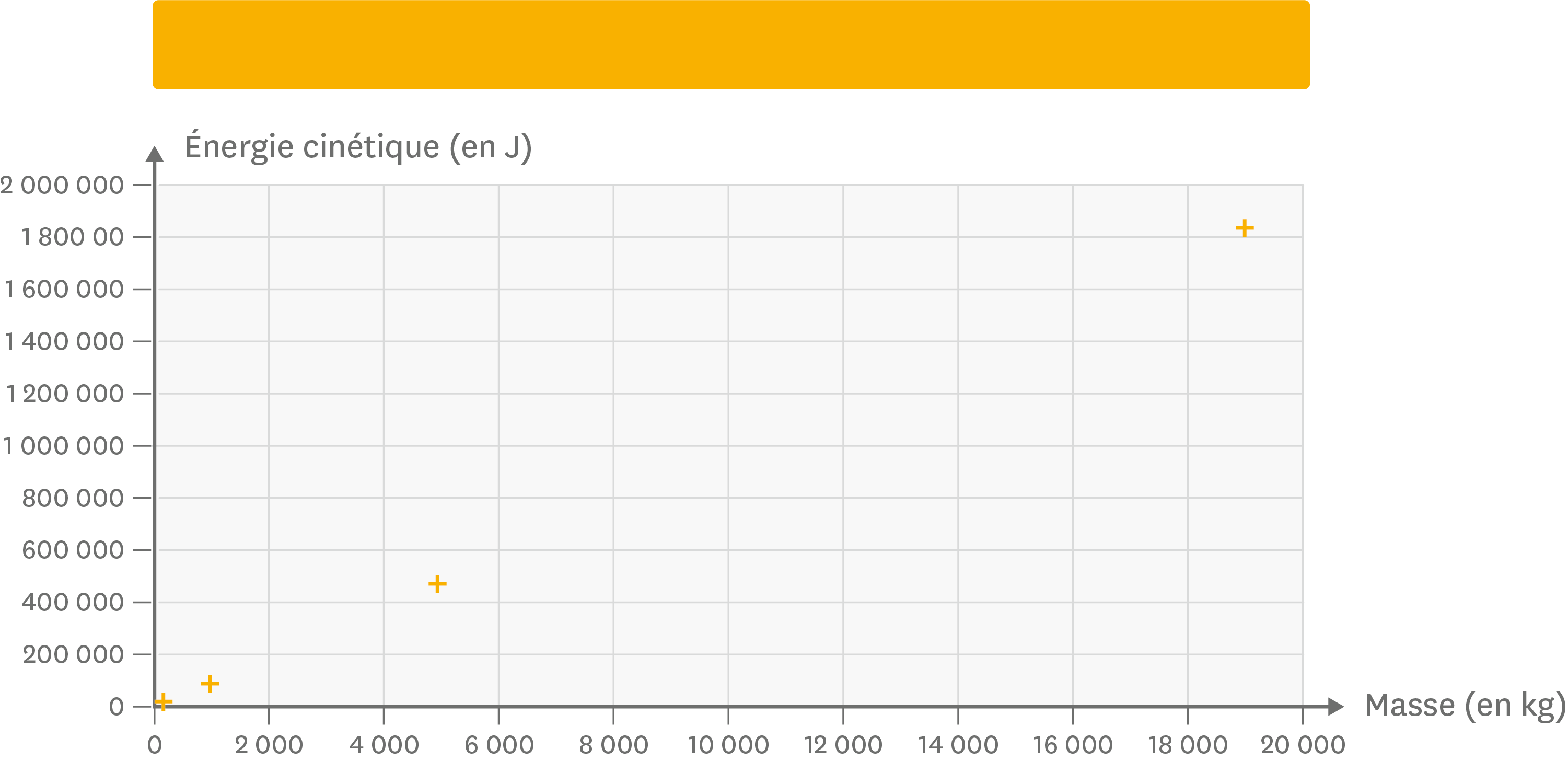
On observe que les points sont répartis le long d’une droite passant par l’origine. Ainsi, on peut en déduire que l’énergie cinétique d’un mobile est proportionnelle à sa masse.
4 Utilise le graphique pour tracer celui de l’énergie cinétique en fonction du carré de la vitesse du véhicule.
> À partir des valeurs de vitesse du graphique, il est possible dans un premier temps de calculer le carré de la vitesse :
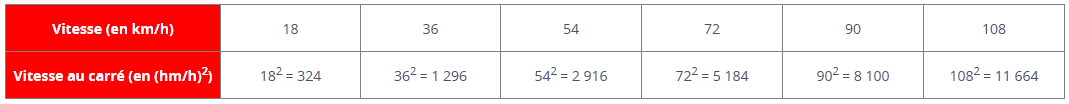
Ensuite, nous pouvons tracer le graphique de l’énergie cinétique en fonction de la vitesse au carré :
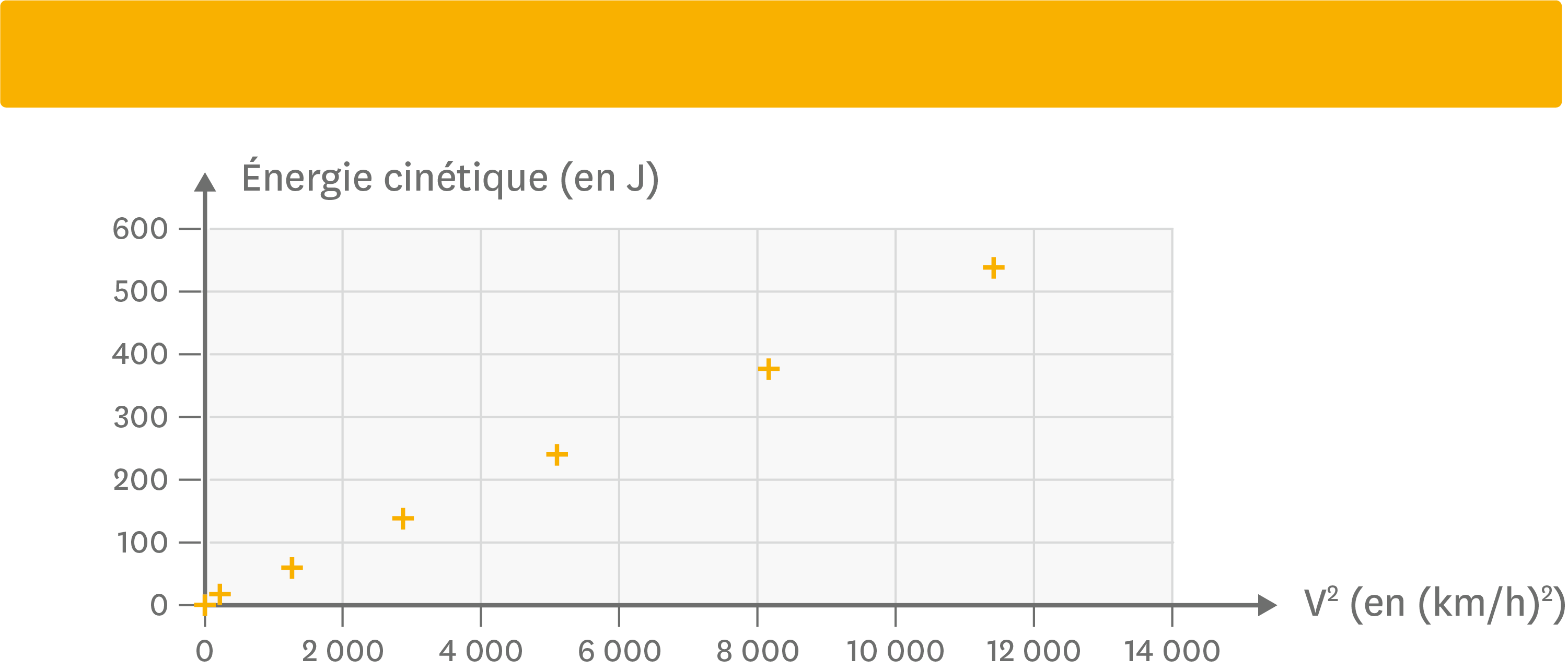
5 Comment l’énergie cinétique est-elle liée au carré de la vitesse ?
> Les points obtenus sont alignés et la droite qui passe au plus près de chacun de ces points, passe aussi par l’origine du repère. Ainsi, nous pouvons déduire que l’énergie cinétique est proportionnelle au carré de la vitesse de l’objet, autrement dit Ec = kv2.

6 D’après ton analyse des données, ton hypothèse était-elle exacte ?
> L’hypothèse de la proportionnalité avec le carré de la vitesse étant très peu probable la réponse la plus fréquente pourrait être : « Non, l’hypothèse n’était pas correcte, car elle n’indiquait pas que l’énergie cinétique est proportionnelle au carré de la vitesse. »
7 Utilise tes résultats et les valeurs issues du graphique pour proposer une expression mathématique de l’énergie cinétique.
> Comme l’énergie cinétique est proportionnelle à la masse, nous pouvons écrire que si seule la masse m est variable : Ec = k × m.
L’énergie cinétique est aussi proportionnelle au carré de la vitesse donc nous pouvons écrire que si seule la vitesse v est variable : Ec = k’ × v2.
Il en découle que lorsque la vitesse v et la masse m sont toutes les deux variables, l’énergie cinétique a pour expression : Ec = k’’mv2.
exercice corrigé 8 p.307 et similaire 9 p.307 (travail en classe)
Livre p.307

- Identifier les différentes formes d’énergie (énergie cinétique, de position, électrique, chimique, thermique, lumineuse, etc.).
- Identifie les réservoirs d’énergie (noyaux, batterie, corps humain, espèces chimiques, etc.).
- Observer l’ordre dans lequel les énergies sont abordées. Cet ordre permet de comprendre comment se fait la conversion d’énergie.
- Pour utiliser l’expression de l’énergie cinétique, vérifier qu’on dispose des bonnes données dans les bonnes unités (J, kg, m/s). Si ce n’est pas le cas, il faut convertir dans ces unités-là.
- Effectuer le calcul numérique en remplaçant chaque grandeur par sa valeur.
parcours de compétences (p.311)
LSU T4.1 Mener une démarche scientifique, résoudre un problème – Pratiquer le calcul numérique et littéral D4
Sur le parcours Paris-Lyon de 430 km, la vitesse de pointe d’un TGV peut être de 300 km/h, soit 83,3 m/s. Son énergie cinétique est alors de 1 340 MJ. Calcule la masse de ce TGV.
Données :
1 MJ = 1 000 000 J.
On sait que Ec = 1/2 × m × v2
Multiplions chaque membre de l’expression par 2 :
2 × Ec = 2 × 1/2 × m × v2
Simplifions le second membre :
2 × Ec = m × v2
Divisons chaque membre par le carré de la vitesse v2 :
2 × Ec / v2 = m × v2 / v2
Simplifions à nouveau le second membre, pour obtenir :
m = 2 × Ec / v2
D’où l’on obtient l’application numérique :
m = 2 × 1340000000 J / (83,3 m/s)2 = 386 229 kg, soit environ 386 tonnes.
activités complémentaires PCCL
l’énergie cinétique : activité scooter et activité QCM
fiches méthodes
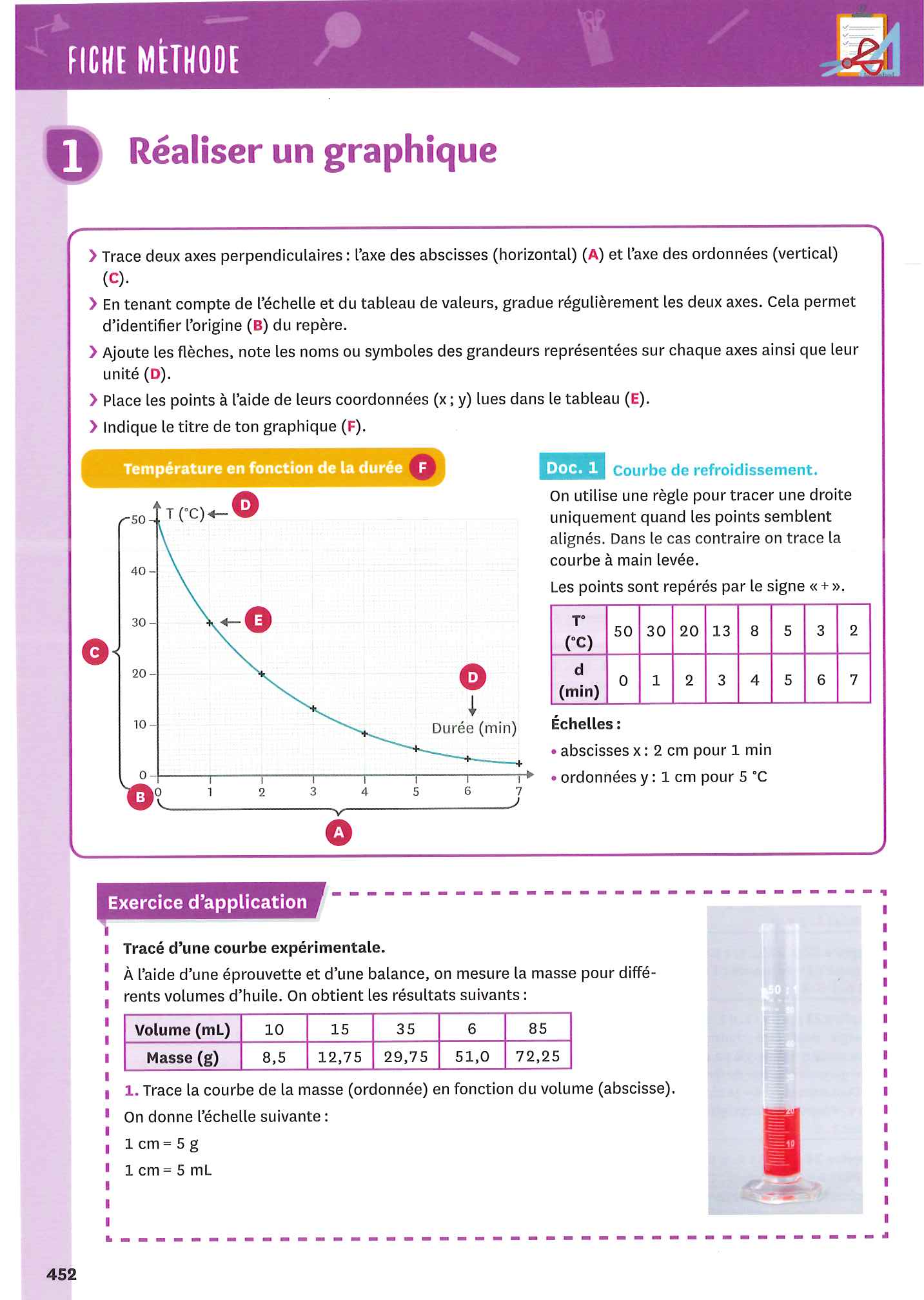

Applications
vérification des connaissances exercices 1,13,16, p.306>
compréhension des connaissances
exercices 22 p.311
22 p.311 : Footing du dimanche
En faisant son footing, Claire, qui a une masse de 50 kg, regarde sa vitesse sur une application de son smartphone. L’application indique 13 km/h.
1. Convertis la vitesse de Claire en m/s.
> Puisque 1 km/h = 1000 / 3600 m/s
alors 13 km/h = 13 × 1 000 / 3 600 ≈ 3,61 m/s.
2. Calcule l’énergie cinétique que possède Claire lors de son footing.
> Pour déterminer l’énergie cinétique de Claire, on fait alors l’application numérique de la relation Ec = 1/ 2 × m × v²
Ec = 0,5 × 50kg × (13 × 1000 / 3600 m/s)²
D’où Ec ≈ 325,8 J.
Lorsque Claire court à 13 km/h, elle possède une énergie cinétique de 324 J.
3. Parfois, Claire ajoute à chaque cheville un bracelet lesté de 1 kg. Calcule la nouvelle masse de Claire ainsi que sa nouvelle énergie cinétique.
> Avec ses bracelets lestées, la masse de Claire passe à 52 kg. Son énergie cinétique devient alors Ec’ ≈ 0,5 × 52kg × (3,61m/s)² ≈ 338,8 J.
4. À quelle vitesse devrait courir Claire pour avoir la même énergie sans bracelets lestés aux chevilles ?
> La vitesse que devrait avoir Claire peut être déduite en isolant la vitesse de l’expression de l’énergie cinétique Ec = 1/ 2 × m × v²
Retrouver la formule de la vitesse à partir de la formule de l’énergie cinétique :
a. Multiplions chaque membre de l’expression par 2 :
2 × Ec = 2 × 1/ 2 × m × v²
b. Simplifions le second membre :
2 × Ec = m × v²
c. Divisons chaque membre par la masse m :
2 × Ec / m = m × v² / m
e. Simplifions à nouveau le second membre :
2 × Ec / m = v²
f. Appliquons une racine carré dans chaque membre pour isoler la vitesse v dans le membre de gauche :
g. Simplifions le premier membre et gardons uniquement la vitesse positive à droite :
\(v=\sqrt{\frac{2 × E_c}{m}}\)h. Remplaçons les symboles par les valeurs de l’énoncé en vérifiant que nous convertissons bien la valeur de la masse en kg :
\(v≈\sqrt{\frac{2 × 338,8J}{50kg}}≈3,68 m/s\)On obtient v = 3,68 m/s
Pour avoir la même énergie cinétique sans porter les bracelets, Claire devrait courir à la vitesse de 3,68 m/s, c’est-à-dire 13,25 km/h (car 3,68 × 3,6 = 13,25km/h).
CDT
3e Univers 12 : Énergie cinétique
https://cours.saettler.org/3u12/
Cours : §1 p.304
Activité 1 p.300 ou Exercice corrigé 8 p.307 et 9 p.307
Exercices 1,13,16, p.306
Programme : E6.1 Identifier les différentes formes d’énergie
» cinétique, potentielle, thermique, électrique, chimique, nucléaire, lumineuse
E6.2 Identifier les sources, les transferts d’énergie pour un système simple
» Sources.
» Transferts.
» Conversion d’un type d’énergie en un autre
E6.3 Établir un bilan énergétique pour un système simple.
» Conservation de l’énergie.» Unités d’énergie.
Devoirs
https://cours.saettler.org/3u12/
Retravailler le cours, les activités, les exercices
Apprendre le cours et le vocabulaire (recopier ou résumer)
Visualiser les activités complémentaires : cours sur PCCL
Faire les exercices : Applications vérification des connaissance 1,13,16, p.306 et 22 p.311


