Plan de cours
consigne : à faire en classe
- Cours (lire et comprendre) : §3 p.258
- Activité 3 p.256
- Vidéos
- Exercices 21 p.260
Devoirs à la maison
- Applications vérification des connaissances
Exercices 3,6,21,24 p.260 - Cours et vocabulaire à apprendre (recopier ou résumer)
- Visualiser les activités complémentaires PCCL, vidéo
Cours et vocabulaire
Isaac Newton a compris au XVIIe siècle qu’il existait toujours une interaction attractive entre deux objets, du fait de leur masse. Il a appelé cette force la force de gravitation.
L’intensité de cette force s’écrit :
Cette force est universelle: on la retrouve en tout lieu et à toute époque de l’Univers.

| Vocabulaire | Définition |
| force de gravitation | force qui permet de comprendre la chute des corps et le mouvement des astres |
Livre
Activités
activités pour comprendre 3 p.256 : Qu’est-ce que la force de gravitation ?
Livre p.256

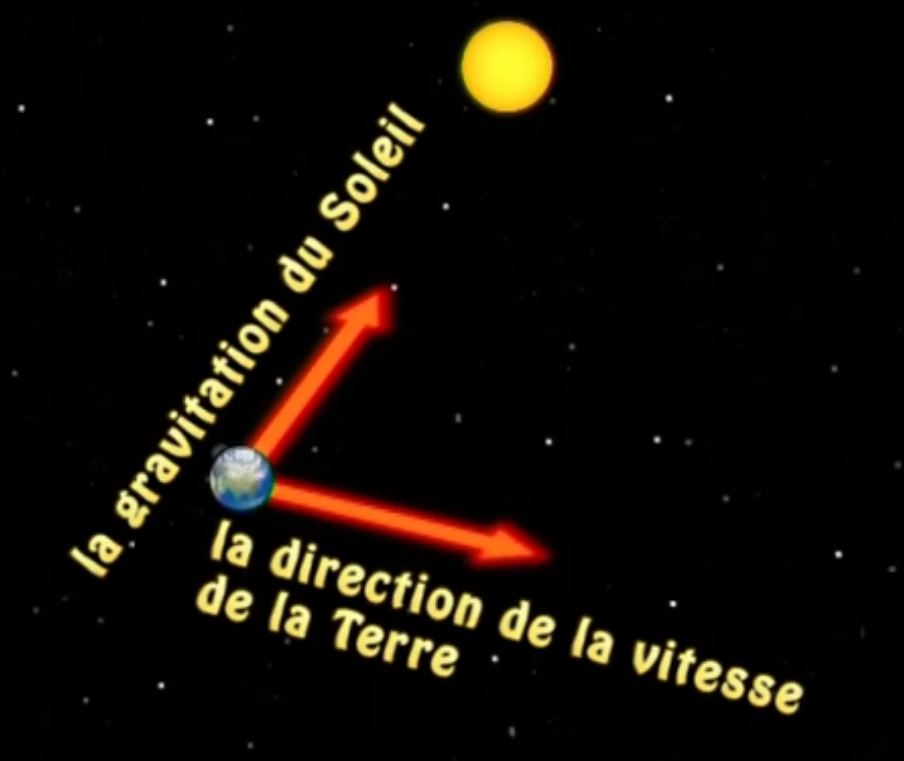
activités complémentaires : vidéos
Applications vérification des connaissances exercices 3,6,21 p.260>
compréhension des connaissances exercices 24 p.263 – Force de gravitation
compétence : T4.1 Mener une démarche scientifique, résoudre un problème – Pratiquer le calcul numérique et littéral D4
Exemple 1 : Ton poids sur la Lune
Le poids d’un objet à la surface d’un astre correspond à la force de gravitation exercée par l’astre sur cet objet.
Données :
- Masse de la Terre : 5,97 × 1024 kg ;
- Rayon de la Terre : 6 370 km ;
- Masse de la Lune : 7,3477 × 1022 kg ;
- Rayon de la Lune : 1 737 km.
Rappel : la force de gravitation a pour valeur
\(\displaystyle F = G × \frac {m_A × m_B} {d^2}\)- avec :
▪ G = 6,67 × 10-11 N.m2/kg2
▪ mA et mB en kg
▪ d en m
1. On note mA ta masse et mB celle de l’astre. Donne la formule que tu vas utiliser pour calculer ton poids sur un astre et justifie ton choix.
> Le poids d’un objet sur un astre est la force d’attraction subie par cet objet à la surface d’un astre. On calcule donc le poids d’un objet selon la formule :
\(\displaystyle P = G × \frac {m_a × m_b} {R^2}\)2. Convertis le rayon de la Terre en mètres.
> 1 km = 1 000 m, donc le rayon de la Terre est : RTerre = 6 370 km = 6 370 × 1 000 m = 6 370 000 m.
3. Calcule PTerre ton poids à la surface de la Terre.
> Pour une personne de masse mA = 70 kg, le poids de cette personne sur Terre est :
\(\displaystyle P_{Terre} = G × \frac {m_a × m_b} {R^2} = 6,67 × 10^{-11} × \frac {70 × 5,97 × 10^{24}} {6 370 000 ^2} = 687 N\)4. Convertis le rayon de Lune en mètres.
> 1 km = 1 000 m, donc le rayon de la Lune est : RLune = 1 737 km = 1 737 × 1 000 m = 1 737 000 m.
5. Calcule PLune ton poids à la surface de la Lune.
> Pour une personne de masse mA = 70 kg, le poids de cette personne sur la Lune est :
\(\displaystyle P_{Lune} = G × \frac {m_a × m_b} {R^2} = 6,67 × 10^{-11} × \frac {70 × 7,3477 × 10^{22}} {1 737 000 ^2} = 114 N \)6. Compare les deux résultats.
> 687÷114 ≈ 6. Le poids sur la Lune sera environ 6 fois plus faible que sur Terre.
Exemple 2 : Ton poids sur Mars
- Masse de la Terre : 5,97 × 1024 kg ;
- Rayon de la Terre : 6 370 km ;
- Masse de Mars : 6,42 × 1023 kg ;
- Rayon de la Mars : 3 390 km.
Rappel : la force de gravitation a pour valeur
\(\displaystyle F = G × \frac {m_A × m_B} {d^2}\)- avec :
▪ G = 6,67 × 10-11 N.m2/kg2
▪ mA et mB en kg
▪ d en m
1. On note mA ta masse et mB celle de l’astre. Donne la formule que tu vas utiliser pour calculer ton poids sur un astre et justifie ton choix.
> Le poids d’un objet sur un astre est la force d’attraction subie par cet objet à la surface d’un astre. On calcule donc le poids d’un objet selon la formule : (où R est le rayon de l’astre en mètres.)
\(\displaystyle P = G × \frac {m_a × m_b} {R^2}\)2. Calcule ton poids à la surface de la Terre.
> On convertit le rayon de la Terre en mètre :
RTerre = 6 370 km = 6 370 × 1 000 m = 6 370 000 m. Pour une personne de masse mA = 70 kg, son poids sur Terre est :
3. Calcule ton poids à la surface de Mars.
> On convertit le rayon de Mars en mètre :
RMars = 3 390 km = 3 390 × 1 000 m = 3 390 000 m. Pour une personne de masse mA = 70 kg, son poids sur Mars est :
Exemple 3 : Est-ce que mon poids change en haut de l’Everest ?
- Masse de la Terre : 5,97 × 1024 kg ;
- Rayon de la Terre : 6 370 km ;
- Hauteur de l’Everest : 8 850 m ;
1. Existe-t-il une différence entre le poids d’un objet et la force de gravitation exercée par la Terre sur cet objet ? Donne la formule qui te permet de calculer la force de gravitation entre deux objets.
> Le poids d’un objet sur un astre est la force d’attraction subie par cet objet à la surface d’un astre. On calcule donc le poids d’un objet selon la formule : (où d est le rayon de l’astre en mètres.)
\(\displaystyle F = G × \frac {m_A × m_B} {d^2}\)2. Calcule ton poids au niveau de la mer et en haut de l’Everest.
> Pour une personne de masse mA = 70 kg, située au niveau de la mer, la distance au centre de la Terre est :
d = RTerre = 6 370 km = 6 370 × 1 000 m = 6 370 000 m.
Donc le poids de cette personne au niveau de la mer est :
Pour une personne de masse mA = 70 kg, située en haut de l’Everest, la distance au centre de la Terre est :
d = RTerre + 8 850 m = 6 370 km + 8 850 m = 6 370 × 1 000 m + 8 850 m = 6 378 850 m.
Donc le poids de cette personne au niveau de la mer est :
La différence de poids entre le niveau de la mer et le haut de l’Everest est très faible.
CDT
3e Univers 7 : La gravitation
https://cours.saettler.org/3u7/
Cours : §3 p.258
Activité 3 p.256
Vidéos
Exercices 21 p.260
Programme : I5.2 Associer la notion d’interaction à la notion de force
I5.3 Exploiter l’expression littérale scalaire de la loi de gravitation universelle, la loi étant fournie.
» Force de pesanteur et son expression P=mg.
Devoirs
https://cours.saettler.org/3u7/
Retravailler le cours, les activités, les exercices
Apprendre le cours et le vocabulaire (recopier ou résumer)
Visualiser les activités complémentaires : fiches méthodes
Faire les exercices : Applications vérification des connaissance 13,6,21,24 p.260
dd


